Two Principles of Multimedia Learning: Redundancy and Split-Attention

Integrating the multimedia assets of a course can raise a host of issues. A client may have slides of text with an out-of-sync voiceover that I need to fix. Or perhaps I must determine whether an animation will be more effective than a series of stills.

Although we know it can be advantageous to present content through multiple forms of media, the big question is how to integrate the mediums.

When deciding on these issues, I rely on two of Richard Mayer’s principles of multimedia learning as guidelines. One is known as the Split-attention Effect and the other is the Redundancy Principle. Here’s how to apply them.

The Redundancy Principle Defined

Redundant Modalities May Interfere with Learning

There is one word of caution when integrating different mediums—avoid redundant content. Redundancy occurs when the same information is presented in multiple formats or modalities. The redundancy effect may reduce rather than increase learning. It places unnecessary demands on a person’s cognitive resources (high cognitive load).

Applying the Redundancy Principle

For example, if you’re displaying a graphic with an audio explanation, avoid also displaying the text of the voiceover. Learners will most likely read the text and miss some of the audio. Rather than using text to call attention to a specific part of a graphic, a simple pointer or other visual cue should suffice.

Put yourself in the place of the learner. Notice the cognitive effort that’s required to perceive, process and comprehend the content you’re presenting. This will give you a sense of which approaches cause cognitive overload and which approaches are well-integrated and promote learning. See The Redundancy Principle in Multimedia Learning for more

Split-attention Principle Defined

The split-attention effect occurs when a person must process two or more varied sources of information simultaneously, either of which can’t be understood in isolation. A typical way this occurs in online learning is when an explanation is displayed on one part of the screen, while a visual, such as a diagram or animation, is presented on another part of the screen.

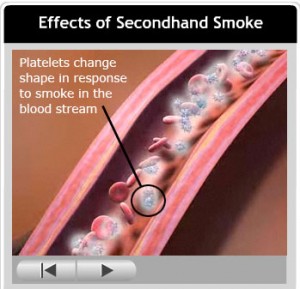
See the frame from an old animation on the right. It shows the effects of secondhand smoke, produced by the Centers for Disease Control. Although the animation was well-done, the viewer had to hold the textual explanation in working memory, while watching the visual.

This type of cognitively demanding task will result in losing some of the information needed to understand both sources of content, causing difficulties in processing the material. To compensate, most people will shift their attention back and forth, which many find frustrating.

See this Split Attention Effect definition for more.

Applying the Split Attention Principle

Integrate Text with Animation—Carefully

The main fix for avoiding the split-attention effect is to integrate the media so that learners don’t need to process disparate sources of information simultaneously. For example, in the above sample, the artist can remove the text explanation from appearing below the graphic. Instead, the artist can place short phrases directly in the animation, as shown in the mock-up here.

You must also be careful that the viewer doesn’t miss the animation while reading the on-screen text. As a safeguard, you can briefly slow down or stop the animation during the display of text. In addition, add user controls for pausing and stopping the animation.

Replace One Modality with Another

Another integration approach that may be more effective is to replace one modality with another. For example, the designer can replaced the text-based explanation with well-synchronized audio. Research shows this to be quite effective for learning. When using mixed modalities, learners don’t need to make a huge effort to integrate the information. It’s done for them in the media itself.

Book Recommendation:
Multimedia Learning by Richard E. Mayer